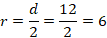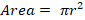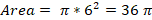3(3x+3)=8x+5 Solve the equation above for x. Which of the following is correct?
A. 1
B. 4
C. -1
D. -4
We use the order of operation to solve for the unknown value of x.
3(3x+3)=8x+5
Multiply 3 with each number in the brackets
(3*3x)+(3*3)=8x+5
9x+9=8x+5
Subtract 9 from both sides
9x+9-9=8x+5-9
9x=8x-4
Subtract 8x on both sides
9x-8x=8x-8x-4
x=-4
Thus, the unknown value of x is -4.
Therefore, the Correct Answer is D.
More Questions on TEAS 7 Math
-
Q #1: 3 (x-2) = 18 Solve the equation above for x. Which of the following is the correct answer?
A. 8
B. -5
C. 7
D. 4
Answer Explanation
We solve for the value of x by following the order of operations
3(x-2)=15
Divide both sides of the equation by 3
Add 2 to both sides of the equation
Thus, the value of x is 8.
-
Q #2: How may milliliters are there in 2.5 liters?
A. 0.25
B. 250
C. 25
D. 2500
Answer Explanation
We use 1 L =1000 mL to convert between the two units. The conversion options of interconversions are:
And
We want millimeters, use the second option to change L to mL as:
Therefore, 2.5 L is equivalent to 2500 mL.
-
Q #3: An athlete runs 7 miles in 45 minutes and then changes their pace to run the next 3 miles in 15 minutes. Overall, what is the average time in minutes it takes the athlete to run 1 mile?
A. 9.5 minutes
B. 9 minutes
C. 6 minutes
D. 10minutes
Answer Explanation
to find the average time the athlete runs in 1 mile; we find total distance and total time the athlete takes in running.
Total distance run by athlete=7+3=10 miles
Total time=45+15 =60 minutes
The athlete runs 10 miles in 60 minutes. For the athlete to cover 1 mile, he will run for a time less than 60 minutes. Thus, in 1 mile, the athlete takes:
So, in 6 minutes, the athlete covers 1 mile.
