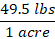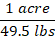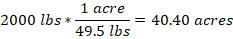A recipe calls for 2.5 teaspoons of vanilla, 1 teaspoon equals approximately 4.93 mL. Which of the following is the correct amount of vanilla in mL?
A. 12.325 mL
B. 5.32 mL
C. 7.43 mL
D. 0.507 mL
We are given that 1 teaspoon=4.93 mL, we can interpret it as:
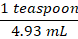
Or
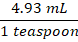
Since we are to find the amount in mL, we look for an option that will cancel teaspoon and remain with mL. The second option is the required conversion, and we proceed as follows:
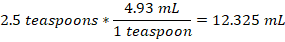
Therefore, 2.5 teaspoons hold about 12.325 mL.
Therefore, the Correct Answer is A.
More Questions on TEAS 7 Math
