An athlete can run 6 miles in 51 minutes. At this rate, how many miles could the athlete run in 90 minutes?
A. 15 miles
B. 11.5 miles
C. 45 miles
D. 10.6 miles
Here, the athlete runs 6 miles in 51 minutes, which can be expressed as:
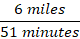
Now, in 90 minutes, the athlete will cover about
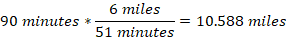
Therefore, the athlete runs about 10.6 miles in 90 minutes.
Therefore, the Correct Answer is D.
More Questions on TEAS 7 Math
-
Q #1: An employee discovers that 0.0025 of all products produced at a factory contain defects. Which of the following percentage does this represent?
A. 0.25%
B. 25%
C. 2.5%
D. 0.025%
Answer Explanation
all products represent 100%. Then, the portion of defect products is:
0.0025 of 100%
‘of’ means multiply
0.0025 *100%=0.25%
-
Q #2: A farmer needs to buy fertilizer for his farmland. The instructions on the bag of the fertilizer say 49.5 pounds of fertilizer is needed for 1 acre of land. The farmer buys 2,000 pounds of fertilizer. Which of the following is the approximate number of acres he can cover with the fertilizer he bought?
A. 40
B. 120
C. 300
D. 1000
Answer Explanation
From the given problem,
49.5 pounds of fertilizer is needed to farm 1 acre of land. This can be interpreted as:
Or
Now we are needed to find the acres of land that will be farmed using 2000 pounds of fertilizers. To solve this, we use the second option as follows:
2000 pounds of fertilizers can farm approximately 40 acres of land.
-
Q #3: A patient drives 19 miles one way to a medical facility for treatment. How far does the patient drive round-trip in 22 days of treatment?
A. 1,254 miles
B. 1,672 miles
C. 418 miles
D. 836 miles
Answer Explanation
Round trip means to and from, which is twice the distance from home to a medical facility.
In one day, the round trip=19+19=38 miles
So, in 22 days, the round trip=38*22=836 miles.
The patient will cover 836 miles in 22 days.
