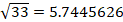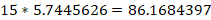/

Joe’s uncle is eight less than four times Joe’s age. Which of the equations represents Joe’s uncle’s age (u) as it relates to Joe’s age (k)?

A. u=8-4k

B. k=4u-8

C. k=8-4u

D. u=4k-8

Answer Explanation:

We are asked to form an equation to find Joe’s uncle’s age to the age of Joe.

First, we find Joe’s age which is k. We know that Joe’s uncle’s age is four times that of Joe less 8. Then,

Joe’s uncle’s age, u = 4k-8.

Thus, the age of Joe’s uncle is u=4k-8.

Therefore, the Correct Answer is d.

Q #1: The length of a rectangular room is 2 feet greater than its width. Which of the following equations represents the area (A) of the room?

A. A=x(x+2)

B. A=2x+2(x+2)

C. A=2x(x+2)

D. A=2x

Answer Explanation
Q #2: Which of the following is the decimal equivalent of 9/25?

A. 36

B. 0.36

C. 3.6

D. 0.25

Answer Explanation

9/25 is the same as 9÷25. Using the calculator, we get 0.36.

Thus, 9/25 in decimal form is 0.36.
Q #3: The American with Disabilities Act (ADA) requires that the slope of a wheelchair ramp be no greater than 1:10. Which of the following is the minimum length of a ramp needed to provide access to a door that is 2.3 feet above the sidewalk?

A. 23 feet

B. 14 feet

C. 32 feet

D. 30 feet

Answer Explanation

Free Access on TEAS 7 Exams and Study Notes

Access to all TEAS 7 Exams
Performance Tracking and Analysis
Well Documented and Explained Questions and Answers
2000+ Questions and Correct Answers: Answers Well Explained
Libary of Detailed StudyNotes
Topical Questions and Answers on Examinable topics

Join Now