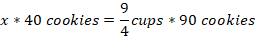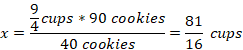The length of a rectangular room is 5 feet greater than its width. Which of the following equations represents the area (A) of the room?
A. A=w+(w+5)
B. A=2w+2(w+5)
C. A=5(w+8)
D. A=w(w+5)
To find the area of the room, we form an equation of find an equation relating the length and width of the rectangle. If we let the width of the room to be w, then
Width of the rectangle= w
Length of rectangle=(w+5)
Area of the rectangle, A= Length*width=(w+5)*w
A=w(w+5)
Thus, the area of the rectangular room is w(w+5).
Therefore, the Correct Answer is D.
More Questions on TEAS 7 Math
-
Q #1: A recipe calls for 3 teaspoons of vanilla. 1 teaspoon equals approximately 4.93 mL. Which of the following is the correct amount of vanilla in mL?
A. 34.33 mL
B. 9.58 mL
C. 10.49 mL
D. 14.79 mL
Answer Explanation
To find the amount of vanilla in mL, use dimensional analysis of the units of measurements.
Two ways to convert between teaspoon and mL are:
Since we are required to find the amount in mL, we use a cionverstioon that will result in mL. Inspecting the above options, we use the second option and set up an equation in way the unwanted units cancel out and leave the wanted unit we are looking for. Then,
Thus, a recipe of 3 teaspoons equals 14.79 mL.
-
Q #2: Which of the following is the decimal equivalent of 15/27? (Round your answer to 2 decimal places).
A. 0.56
B. 5.56
C. 3.86
D. 0.36
Answer Explanation
Using a calculator to evaluate 15÷27 results in 0.5555555556. To two decimal places, the answer becomes 0.56.
Thus, 0.56 is the decimal equivalent of 15/27.
-
Q #3: A bag contains six green balls, eight red balls, and three yellow balls. If one ball is randomly selected from the ball, which of the following is the probability that the ball is green?
A. 10/17
B. 3/17
C. 2/17
D. 6/17
Answer Explanation
The probability of finding a green ball is given by
Total number of balls in the bag=6+8+3=17 balls
Therefore, the probability of drawing a green ball from the bag containing 17 balls is 6/17.
